7 algoritmai, kuriuos turėtų žinoti kiekvienas programuotojas

Kaip programavimo studentas, greičiausiai per savo karjerą išmokote daug įvairių algoritmų. Bet kuriam programuotojui būtina mokėti mokėti įvairius algoritmus.

Turint tiek daug algoritmų, gali būti sudėtinga sekti tai, kas svarbiausia. Jei ruošiatės pokalbiui ar tiesiog tobulinate savo įgūdžius, šis sąrašas bus gana lengvas. Skaitykite toliau, kai išvardijame svarbiausius programuotojų algoritmus.

1. Dijkstros algoritmas

Edsgeris Dijkstra buvo vienas įtakingiausių savo laiko kompiuterių mokslininkų, ir jis prisidėjo prie to daug įvairių kompiuterijos mokslo sričių, įskaitant operacines sistemas, kompiliatoriaus konstrukciją ir daug daugiau. Vienas žymiausių Dijkstros indėlių yra jo trumpiausio grafikų algoritmo, dar vadinamo Dijkstros trumpiausio kelio algoritmu, išradingumas.

„Dijkstra“ algoritmas nustato trumpiausią grafiko kelią nuo šaltinio iki visų grafiko viršūnių. Prie kiekvieno algoritmo kartojimo pridedama viršūnė su mažiausiu atstumu nuo šaltinio ir ta, kurios nėra dabartiniame trumpiausiame kelyje. Tai godus turtas, kurį naudoja Džikstros algoritmas.

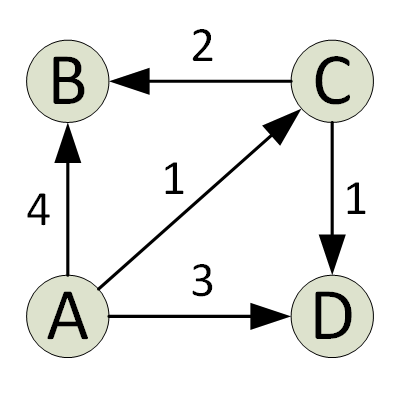
Paprastai algoritmas įgyvendinamas naudojant rinkinį. „Dijkstra“ algoritmas yra labai efektyvus, kai įgyvendinamas naudojant „Min Heap“; trumpiausią kelią galite rasti tik per O (V+ElogV) laiką (V yra viršūnių skaičius, o E - briaunų skaičius tam tikrame grafike).

„Dijkstra“ algoritmas turi savo apribojimų; jis veikia tik nukreiptuose ir nenukreiptuose grafikuose su teigiamo svorio kraštais. Esant neigiamiems svoriams, pirmenybė teikiama „Bellman-Ford“ algoritmui.

Interviu klausimai paprastai apima „Djikstra“ algoritmą, todėl labai rekomenduojame suprasti sudėtingas jo detales ir programas.

2. Sujungti Rūšiuoti

Šiame sąraše yra keletas rūšiavimo algoritmų, o sujungimo rūšiavimas yra vienas iš svarbiausių algoritmų. Tai efektyvus rūšiavimo algoritmas, paremtas „Dalink ir užkariauk“ programavimo technika. Blogiausiu atveju sujungimo rūšiavimas gali surūšiuoti „n“ skaičius tik per O (nlogn) laiką. Palyginti su primityviais rūšiavimo būdais, tokiais kaip Rūšiuoti burbulus (tai užtrunka O (n^2) laiko), sujungimo rūšiavimas yra labai efektyvus.

Susijęs: Įvadas į sujungimo rūšiavimo algoritmą

Sujungiant rūšiavimą, masyvas, kurį reikia rūšiuoti, pakartotinai suskaidomas į antrinius masyvus, kol kiekvieną dalinę masyvą sudaro vienas skaičius. Tada rekursinis algoritmas pakartotinai sujungia antrinius masyvus ir rūšiuoja masyvą.

3. „Quicksort“

„Quicksort“ yra dar vienas rūšiavimo algoritmas, pagrįstas „Dalink ir valdyk“ programavimo technika. Pagal šį algoritmą elementas pirmiausia pasirenkamas kaip šarnyras, o tada visas masyvas yra padalintas aplink šį sukamąjį tašką.

Kaip jūs tikriausiai atspėjote, geras sukimasis yra labai svarbus efektyviam rūšiavimui. Sūkurys gali būti atsitiktinis elementas, laikmenos elementas, pirmasis elementas arba net paskutinis elementas.

„Quicksort“ diegimai dažnai skiriasi tuo, kaip jie pasirenka šerdį. Paprastai „quicksort“ surinks didelį masyvą su geru pasukimu tik per O (nlogn) laiką.

Bendras greitojo pseudokodo pakartotinai padalijamas masyvas į sukamąjį tašką ir nustatomas į teisingą papildomosios masyvo padėtį. Ji taip pat įdeda elementus, mažesnius už sukamąją dalį kairėje, ir elementus, didesnius už ašį dešinėje.

4. Gylis Pirmoji paieška

„Depth First Search“ (DFS) yra vienas iš pirmųjų grafikų algoritmų, mokomų studentams. DFS yra efektyvus algoritmas, naudojamas pereiti ar ieškoti grafiko. Jis taip pat gali būti modifikuotas, kad jį būtų galima naudoti važiuojant medžiu.

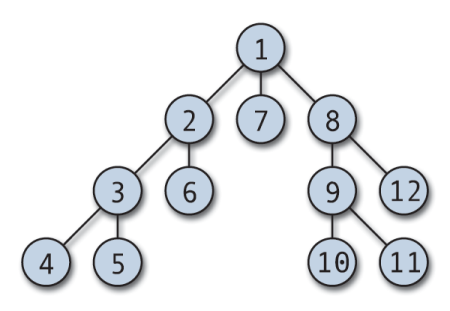
DFS pravažiavimas gali prasidėti nuo bet kurio savavališko mazgo ir neria į kiekvieną gretimą viršūnę. Algoritmas grįžta atgal, kai nėra neaplankytos viršūnės arba yra aklavietė. DFS paprastai diegiamas su krūva ir logine masyvu, kad būtų galima stebėti lankomus mazgus. DFS yra paprasta įdiegti ir išskirtinai veiksminga; jis veikia (V+E), kur V yra viršūnių skaičius, o E - kraštų skaičius.

Įprastos DFS sekimo programos apima topologinį rūšiavimą, ciklų aptikimą grafike, kelio paiešką ir stipriai sujungtų komponentų paiešką.

5. Plotis-pirmoji paieška

„Pločio pirmoji paieška“ (BFS) taip pat žinoma kaip medžių lygių eilių perėjimas. BFS veikia O (V+E), panašiai kaip DFS algoritmas. Tačiau BFS vietoj krūvos naudoja eilę. DFS pasineria į grafiką, o BFS pereina grafiką pločio kryptimi.

BFS algoritmas naudoja eilę, kad galėtų stebėti viršūnes. Nelankomos gretimos viršūnės lankomos, pažymimos ir eilėje. Jei viršūnėje nėra gretimos viršūnės, tada viršūnė pašalinama iš eilės ir ištiriama.

BFS dažniausiai naudojamas lygiaverčiuose tinkluose, trumpiausiu nesverto grafiko keliu ir nustatant mažiausią apimantį medį.

6. Dvejetainė paieška

Dvejetainė paieška yra paprastas algoritmas norimam elementui surasti surūšiuotame masyve. Tai veikia pakartotinai padalijus masyvą per pusę. Jei reikalingas elementas yra mažesnis už vidurinį elementą, tada kairioji vidurinio elemento pusė apdorojama toliau; priešingu atveju dešinė pusė perpus ir vėl ieškoma. Procesas kartojamas, kol randamas reikiamas elementas.

Blogiausiu atveju dvejetainės paieškos sudėtingumas yra O (logn), todėl jis yra labai efektyvus ieškant tiesinių masyvų.

7. Minimalūs išplėtimo medžio algoritmai

Minimalus schemos slenksčio medis (MST) turi mažiausią kainą tarp visų galimų apimančių medžių. Slenkančio medžio kaina priklauso nuo jo kraštų svorio. Svarbu pažymėti, kad minimalus apimantis medis gali būti daugiau nei vienas. Yra du pagrindiniai MST algoritmai, būtent Kruskal ir Prim.

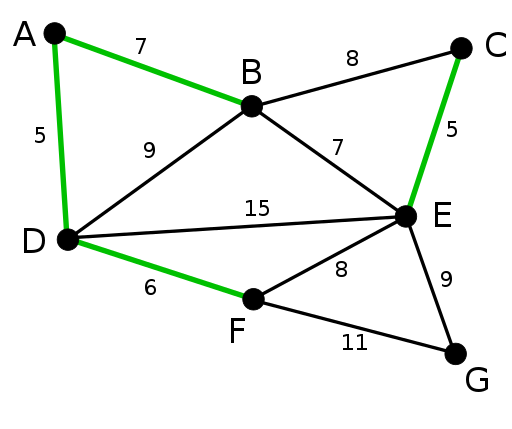
„Kruskal“ algoritmas sukuria MST, pridedant prie augančio rinkinio kraštą su minimaliomis sąnaudomis. Algoritmas pirmiausia surūšiuoja kraštus pagal jų svorį ir tada prideda kraštus prie MST, pradedant nuo minimalaus.

Svarbu pažymėti, kad algoritmas neprideda briaunų, sudarančių ciklą. Retiems grafikams pirmenybė teikiama Kruskalio algoritmui.

„Prim“ algoritmas taip pat naudoja godžią savybę ir idealiai tinka tankiems grafikams. Pagrindinė „Prim“ MST idėja yra turėti du skirtingus viršūnių rinkinius; viename rinkinyje yra auganti MST, o kitame - nepanaudotos viršūnės. Kiekvienos kartojimo metu pasirenkamas mažiausias svorio kraštas, kuris sujungs du rinkinius.

Minimalūs aprėpties medžio algoritmai yra būtini klasterių analizei, taksonomijai ir transliavimo tinklams.

Efektyvus programuotojas išmano algoritmus

Programuotojai nuolat mokosi ir tobulina savo įgūdžius, ir yra keletas esminių dalykų, kuriuos visi turi mokėti. Kvalifikuotas programuotojas žino skirtingus algoritmus, kiekvieno naudą ir trūkumus ir kuris algoritmas būtų tinkamiausias konkrečiam scenarijui.

Įvadas į apvalkalo rūšiavimo algoritmą

Nors apvalkalo rūšiavimas nėra pats efektyviausias metodas, pradedantieji turi daug naudos iš jo praktikavimo.

Skaityti toliau

Apie autorių